Blog de una profe ingeniera---No os vayáis por la tangente
domingo, 27 de diciembre de 2015
LEY DE LOS SENOS
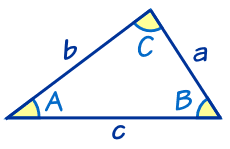
La ley de los senos establece que en cualquier triángulo la relación de cualquiera de sus lados al seno del ángulo opuesto es constante.
Escrita como fórmula, la ley de los senos es la siguiente:
a / sen A = b / sen B = c / sen C
APLICACIÓN
1)Resolver el siguiente triángulo:
El tercer ángulo del triángulo es:
C = 180° – A – B = 180° – 30° – 20 ° = 130°
Por la ley de los senos:
Por las propiedades de las proporciones:
2) Resolver el siguiente triángulo:
El tercer ángulo del triángulo es:
C = 180° – A – B = 180° – 42° – 75° = 63°
Por la ley de los senos:
Por las propiedades de las proporciones:
RAZONES TRIGONOMÉTRICAS
sen α= cateto opuesto / hipotenusa = co / h
cos α= cateto contiguo / hipotenusa = cc /h
tg α= cateto opuesto / cateto contiguo = co /cc
Vamos a utilizar las razones trigonométricas para ver cómo se resuelven algunos triángulos rectángulos:
* Dado un lado y un ángulo:
En este caso nos dan el ángulo y la hipotenusa de manera que podemos usar el seno y el coseno para hallar los lados que faltan:
sen 26= cateto opuesto / hipotenusa = co / 45
pasamos el 45 multiplicando de manera que
co=45*sen26= 19.73
Ya tenemos:
Ahora hay varias maneras de proceder. Podríamos calcular el cateto contiguo al ángulo de 26º utilizando la fórmula del coseno, esto es:
cos 26 = cateto contiguo / hipotenusa = cc / 45
pasamos el 45 multiplicando de manera que
cc = 45*cos 26 = 40.44.
O podríamos utilizar el teorema de pitágoras: la hipotenusa al cuadrado es igual a la suma de los catetos cada uno de ellos al cuadrado, esto es,
45² = 19.73² + cc²
cc² = 45²-19.73²
y haciendo la raíz cuadrada obtenemos el mismo resultado
cc = 40.44.
Nos será indiferente utilizar un método u otro.
SENO Y COSENO
El chiste:
A: Estoy algo preocupada por la obsesión de Math por encontrar a diferencia entre seno y coseno
B: No te preoocupes. Solo es una fase. jejeje
Muy gracioso y... cierto también.
No es mi intención confundir al lector cuando digo que seno y coseno son lo mismo sino explicar por qué se dice esto.
Cuando representamos la función sen(x) en una gráfica de manera que le damos todos los valores posibles a x y vemos qué se obtiene para sen(x) obtenemos esto:
donde si representamos los puntos A = sen(0)=0, B= sen(1) = 0.84, C=sen(2) = 0.92, D= sen(3)=0.14, E= sen(4) = -0.76 y F=sen(5) = -0.96 se puede obtener una vista más clara de lo que digo.
Sin embargo, cuando del mismo modo representamos la función coseno(x) se obtiene:
que no es otra cosa que un "seno desplazado" con un "desplazamiento de fase" (de ahí el chiste).
¿Cuánto se desplaza? Se desplaza exactamente una distancia de Π/2, es decir, si representamos ahora sen(x+Π/2):
¿Sorprendente? ¡Se obtiene lo mismo! Pruéblao con tu calculadora.
sen(x + Π/2) = cos(x) para todo x.
Esto quiere decir que: sen(1 + Π/2) = cos(1) , sen(2.33 + Π/2) = cos(2.33), etc.. (tan largo como la cantidad de números reales que existen).
Suscribirse a:
Entradas (Atom)