HIPNOTÍZATE
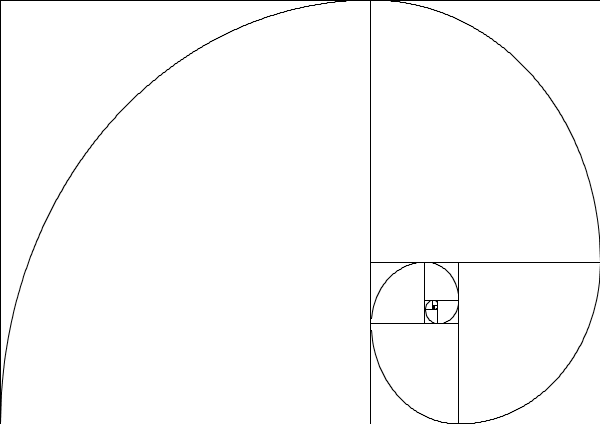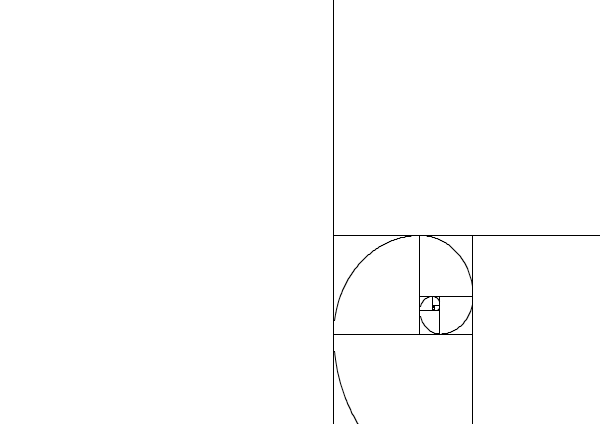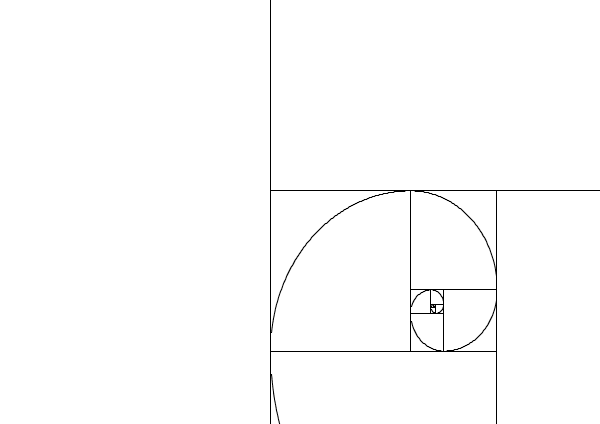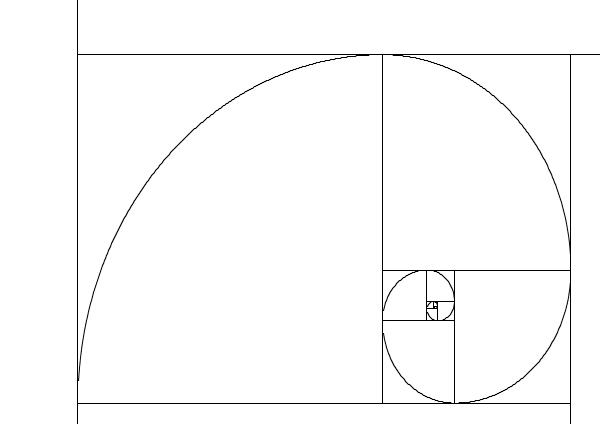
La espiral, serie de Fibonacci o secuencia áurea es muy conocida en el mundillo matemático. A finales del s. XII, el matemático italiano Leonardo de Pisa (1170-1240), quien era más conocido por Fibonacci o hijo de Bonaccio, un antigo conocido mercader de la ciudad de Pisa que poseía negocios en el norte de África, describió esta fórmula como solución a un problema de la cría de conejos.
La conocida espiral, denominada "sucesión de Fibonacci" aparece constantemente en la naturaleza.
Esta secuencia tan querida por los aficionados a las matemáticas, se forma sumando los dos elementos anteriores de la serie, es decir, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… Aparentemente, podría resultar una serie matemática cualquiera, sin más relevancia, pero no. Además de ser muy importante en la aplicación de diversas teorías (ciencias de la computación, matemáticas, configuraciones biológicas y teoría de juegos), es muy curioso y no deja de llamar la atención, como esta serie aparece en la naturaleza de una forma óptica.
La sucesión de esta serie, se inicia con 0 y 1 y a partir de ahí cada elemento es la suma de los dos anteriores. A cada elemento que forma esta sucesión se le denomina número de Fibonacci.
En la práctica se usa mucho para termodinámica, mecánica de fluidos, arquitectura, diseño de turbinas y bombas....
Y todo comenzó con un problema de cría de conejos. Era el siquiente:
"Cierto hombre tenía una pareja de conejos juntos en un lugar cerrado y uno desea saber cuántos son creados a partir de este par en un año cuando es su naturaleza parir otro par en un simple mes, y en el segundo mes los nacidos parir también."
Como podéis comprobar en la imagen, el número de parejas a lo largo de los meses coincide con los términos enunciados en la sucesión. Más simplificado: la secuencia sirve para conocer el número de parejas conejos que habrá en doce meses y también para saber si estos se reproducen continuamente, así como si cada pareja de conejos produce una nueva pareja de conejos (un macho y una hembra). Cada conejo se puede cruzar a la edad de un mes, siendo su periodo de gestación un mes.
La conocida espiral, denominada "sucesión de Fibonacci" aparece constantemente en la naturaleza.
Esta secuencia tan querida por los aficionados a las matemáticas, se forma sumando los dos elementos anteriores de la serie, es decir, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… Aparentemente, podría resultar una serie matemática cualquiera, sin más relevancia, pero no. Además de ser muy importante en la aplicación de diversas teorías (ciencias de la computación, matemáticas, configuraciones biológicas y teoría de juegos), es muy curioso y no deja de llamar la atención, como esta serie aparece en la naturaleza de una forma óptica.
La sucesión de esta serie, se inicia con 0 y 1 y a partir de ahí cada elemento es la suma de los dos anteriores. A cada elemento que forma esta sucesión se le denomina número de Fibonacci.
En la práctica se usa mucho para termodinámica, mecánica de fluidos, arquitectura, diseño de turbinas y bombas....
El famoso problema de los conejos
Y todo comenzó con un problema de cría de conejos. Era el siquiente:
"Cierto hombre tenía una pareja de conejos juntos en un lugar cerrado y uno desea saber cuántos son creados a partir de este par en un año cuando es su naturaleza parir otro par en un simple mes, y en el segundo mes los nacidos parir también."
Como podéis comprobar en la imagen, el número de parejas a lo largo de los meses coincide con los términos enunciados en la sucesión. Más simplificado: la secuencia sirve para conocer el número de parejas conejos que habrá en doce meses y también para saber si estos se reproducen continuamente, así como si cada pareja de conejos produce una nueva pareja de conejos (un macho y una hembra). Cada conejo se puede cruzar a la edad de un mes, siendo su periodo de gestación un mes.
Problema de los conejos




No hay comentarios:
Publicar un comentario